つれづれなるままに

_ [アニメ] 理系が恋に落ちたので証明してみた。r=1-sinθ(第2期)

初回。

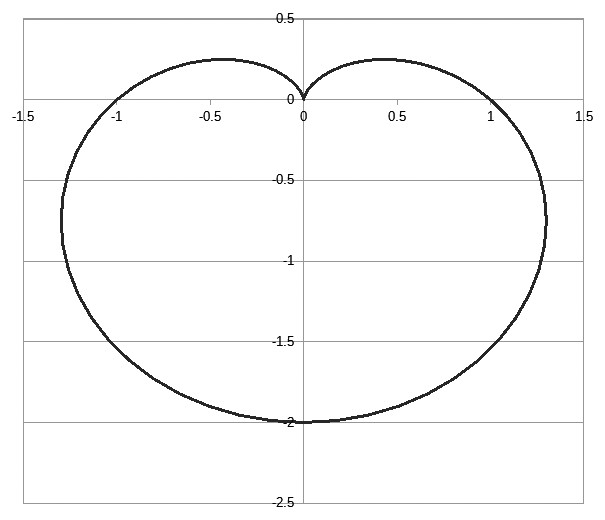
この $r=1-\sin\theta$ というのは極方程式というやつのひとつで、カージオイド曲線 cardioid というらしい。(実際は $r=1+\cos\theta$ の方がカージオイドみたいですが。横倒しの形になります。)

右のは Libreoffice の Calc で描いたこの曲線です。

要するにグラフ化するとハート型みたいな形になる、というやつです。

ま、そういうこと。

カージオイド曲線は καρδιά (心臓) と είδος (形) から来てる言葉だそうで。

角度が $\theta$ のときに原点からの距離が $r$ になるので、簡単に x-y 座標に変換できます。

$$x = r\cos\theta = (1-\sin\theta)\cos\theta$$

$$y = r\sin\theta = (1-\sin\theta)\sin\theta$$ とすれば、あとは $\theta$ に 0～2π の数値を入れてグラフ化すれば右の図ができあがります。

といった甘々な(?)話がまた始まるのでした。

初回は1期のラストのオキシトシンのエピソードを引き摺ってのもの。でも、最近はオキシトシンがそこまで確実に気持を表わしてるかというのはわからないのだ、という話がありますがね。

_ [アニメ] 現実主義勇者の王国再建記 第2期

最終話。

前王に呼び出されたソーマですが、そこでソーマに王位が譲位された理由について前王に聞かされるのでした。

ここまでファンタジーですらなく、普通の王国再建記的な雰囲気を持っていたこの話ですが、一挙にSFな話になってきました。

タイムリープが全ての鍵になっていたと。

そんな感じ。

うまくまとめたというところでしょうか。